Bir strateji oyununun temelinde, oyuncuların kararlarının karşılıklı bağımlı olması yatar. Bu karşılıklı etkileşimler iki yolla ortaya çıkar: Birincisi, hamleler art arda gelir yani ardışıktır. Oyuncular hamleleri sırayla yaparlar. İkinci tür karşılıklı etkileşim ise tutuklular ikileminde olduğu gibi eş zamanlıdır. Oyuncular aynı anda, ötekinin o sıradaki eylemlerini bilmeksizin karar verir ve hareket eder.
Bir stratejik etkileşimin ardışık mı, eşzamanlı mı olduğunu kestirmek önemlidir. Bazı etkileşimlerde her iki öğeyi de bulabilirsiniz.
Ardışık hamlelerin yer aldığı bu oyunda genel ilke şöyledir: Her oyuncu, öteki oyuncuların gelecekteki karşı hareketlerini hesaplamalı ve bunları şimdiki kendi en iyi hamlesini hesaplamakta kullanmalıdır. Bu fikir o kadar önemlidir ki, stratejik davranmanın bir temel kavramı olarak ifade edilir.
Kural: İleriye doğru bak ve geriye doğru akıl yürüt.
Başlangıçtaki kararların sizi en sonunda nereye götüreceğini öngördükten sonra, bu bilgiyi en iyi seçiminizi belirlemekte kullanabilirsiniz.
Karar Ağacı
İleriye bakıp geriye akıl yürütmek gerektiren bir dizi karar, başkalarıyla strateji oyunu oynamayan tek bir karar verici için ortaya çıkabilir. Acil Tıpta pek çok yerde kullandığımız algoritmalar buna örnektir. Örneğin pulmoner emboli‘yi düşündüğümüzde Wells skorlamasıyla başlayan pek çok yol kendi dallarına ayrılarak ilerler. Her kavşak noktasındaki seçenekleri gösteren bu yol haritası ard arda çıkan dallarla bir ağaca benzemektedir. Bu nedenle karar ağacı ismini alır.
Benzer bir karar ağacı örneğini ulaşım alanından verebiliriz. İstanbul Anadolu yakasından Avrupa yakasına geçişte kullanılabilecek yolları bir karar ağacında gösterirsek:
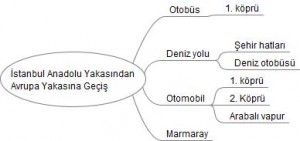
Karşıya geçerken en iyi rotayı seçmek gideceğiniz yere ve zamana bağlıdır. Eğer Galatasaray’ın maçına gidiyorsanız 2. köprüyü kullanarak otomobille karşıya geçmek Marmaray’ı kullanmaktan daha akılcı olabilir. Burada önce gelecekteki kararımızı öngörür sonra seçimimizi yaparız.
Oyun Ağacı
Bir strateji oyununda seçenekleri görmek için karar ağacı kullanılabilir ama burada bir sorun vardır; bir oyunda iki ya da daha fazla oyuncu vardır. Ağaç boyunca dalların ayrıldığı noktalarda karar verme sırası farklı oyuncularda olabilir. Bu durumda oluşan şemaya aradaki farkı vurgulamak için oyun ağacı denir.
Ardışık hamlelerin özelliği benim rakibimin ne yaptığını tam olarak bildikten sonra hamle yapmam ve rakibimin de benim ne yaptığımı tam olarak bildikten sonra hamle yapmasıdır.
Örneğin bir hasta için tedavisinin düzenlenerek takip edilmesi ya da başka bir kliniğine devredilmesi seçeneği olan bir etkileşimde ilk aşamada şöyle bir şema ortaya çıkabilir:

Bir hasta için birden fazla kliniğin devreye girdiği daha karışık karar ağaçları oluşması olasıdır.
Satranç sırayla oynanan bir oyun olduğu için bir oyun ağacına yerleştirilebilir. İlk birkaç hamleden sonra ağacın ne kadar karmaşıklaştığını görmek zor değildir. Birçok oyunda oyun bir oyuncunun kazanması ya da berabere bitmesiyle sonuçlanır. (Acil tıp için hastanın bir kliniğe devredilmesi ya da kliniklerin berabere kalarak hastanın taburcu olması ile sonuçlanabilir. Tabii bir seçenek de hastanın morga nakledilmesidir.)
Bir oyunda seçilen izlek eğer sonlu sayıda hamle sonra bitecekse, o zaman ilkesel olarak, oyun tamamen çözülebilir. Oyunu çözmek demek, kimin nasıl kazanacağını bulmak demektir. Oyun ağacında geriye doğru akıl yürüterek kimin kazanacağı bulunabilir. Sonlu sayıda bir dizi hamleleri olan herhangi bir oyun için bir en iyi strateji mevcuttur. Bir en iyi stratejinin bulunması bizim onu her zaman kolayca bulabileceğimiz anlamına gelmez. Satranç bunun en iyi örneğidir. Belki klinik pratiğimizde hiçbir kliniğin yatırmayı kabul etmediği hastalarda bir üst otoriteye duyulan ihtiyaç da bundandır.
Kaynaklar:
- Stratejik Düşünme, Avinash K. Dixit, Barry J. Nalebuff;(2002) Sabancı Üniversitesi Yayınları
- Askeri Tarihte Stratejik Düşünce, M. Tanju Akad;(2012) Türkiye İş Bankası Yayınları
- Beş Altın Kural 20. Yüzyıl Matematiğinin Önemli Teorileri; (2000) Sabancı Üniversitesi Yayınları



